6. Cycles & Phasings

:

6.1. Cycles

The WLTC-profiles for the various classes were generated from the tables of the specs above using the devtools/csvcolumns8to2.py script, but it still requires an intermediate manual step involving a spreadsheet to copy the table into ands save them as CSV.

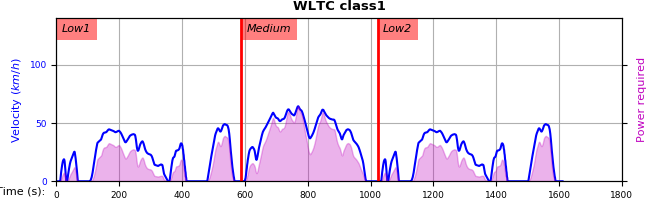
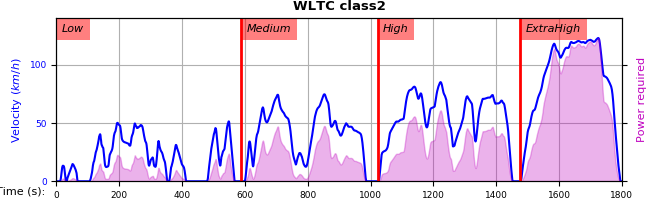
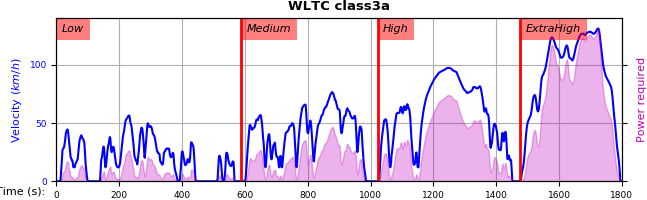
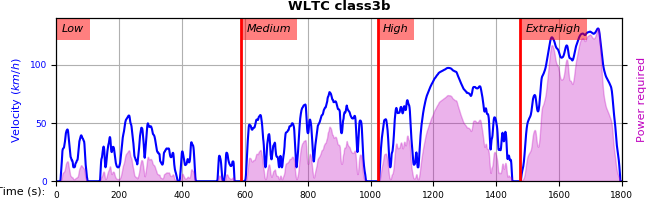
_images/wltc_class1.png _images/wltc_class2.png _images/wltc_class3a.png _images/wltc_class3b.png

6.1.1. Phases (the problem)

6.1.1.1. GTR’s “V” phasings

The GTR’s velocity traces have overlapping split-time values, i.e. belonging to 2 phases, and e.g. for class1 these are the sample-values @ times 589 & 1022:

GTR’s “V” phasing scheme for Velocities

class1

phase-1

phase-2

phase-3

cycle

Boundaries

[0, 589]

[589, 1022]

[1022, 1611]

[0, 1611]

Duration

589

433

589

1611

# of samples

590

434

590

1612

6.1.1.2. “Semi-VA” phasings

Some programs and most spreadsheets do not handle overlapping split-time values like that (i.e. keeping a separate column for each class-phase), and assign split-times either to the earlier or the later phase, distorting thus the duration & number of time samples some phases contain!

For instance, Access-DB tables assign split-times on the lower parts, distorting the start-times & durations for all phases except the 1st one (deviations from GTR in bold):

Access-DB, a “semi-VA1” phasing scheme (all but 1st phases shorter)

class1

phase-1

phase-2

phase-3

cycle

Boundaries

[0, 589]

[590, 1022]

[1023, 1611]

[0, 1611]

Duration

589

432

588

1611

# of samples

590

433

589

1612

Note

The algorithms contained in Access DB are carefully crafted to do the right thing.

The inverse distortion (assigning split-times on the higher parts) would preserve phase starting times (hint: downscaling algorithm depends on those absolute timings being precisely correct):

“Inverted” Access-DB, a “semi-VA0” phasing schema (all but last phases shorter)

class1

phase-1

phase-2

phase-3

cycle

Boundaries

[0, 588]

[589, 1021]

[1022, 1611]

[0, 1611]

Duration

588

432

589

1611

# of samples

589

433

590

1612

6.1.1.3. “VA” phasings

On a related issue, GTR’s formula for Acceleration (Annex 1 3.1) produces one less value than the number of velocity samples (like the majority of the distorted phases above). GTR prescribes to (optionally) append and extra A=0 sample at the end, to equalize Acceleration & Velocities lengths, but that is not totally ok (hint: mean Acceleration values do not add up like mean-Velocities do, see next point about averaging).

Since most calculated and measured quantities (like cycle Power) are tied to the acceleration, we could refrain from adding the extra 0, and leave all phases with -1 samples, without any overlapping split-times:

“VA0” phasings

class1

phase-1

phase-2

phase-3

cycle

Boundaries

[0, 588]

[589, 1021]

[1022, 1610]

[0, 1610]

Duration

588

432

588

1610

# of samples

589

433

589

1611

Actually this is “semi-VA0” phasings, above, with the last part equally distorted by -1 @ 1610. But now the whole cycle has (disturbingly) -1 # of samples & duration:

We can resolve this, conceptually, by assuming that each Acceleration-dependent sample signifies a time-duration, so that although the # of samples are still -1, the phase & cycle durations (in sec) are as expected:

“VA0+” phasings, with 1 sec step duration

class1

phase-1

phase-2

phase-3

cycle

Boundaries

[0, 589 )

[589, 1022 )

[1022, 1611 )

[0, 1611 )

Duration

589

433

589

1611

# of samples

589

433

589

1611

Summarizing the last “VA0+” phasing scheme:

  • each step signifies a “duration” of 1 sec,

  • the duration of the final sample @ 1610 reaches just before 1611sec,

  • # of samples for all phases are symmetrically -1 compared to Velocity phases,

  • it is valid for Acceleration-dependent quantities only,

  • it is valid for any sampling frequency (not just 1Hz),

  • respects the Dijkstra counting (notice the parenthesis signifying open right intervals, in the above table), BUT …

  • Velocity-related quantities cannot utilize this phasing scheme, must stick to the original, with overlapping split-times.

6.1.1.4. Averaging over phases

Calculating mean values for Acceleration-related quantities produce correct results only with non-overlapping split-times.

It’s easier to demonstrate the issues with a hypothetical 4-sec cycle, composed of 2 symmetrical ramp-up/ramp-down 2-sec phases (the “blue” line in the plot, below):

ramp-up/down cycle

t

V-phase1

V-phase2

V

Distance

VA-phase

A

[sec]

[kmh]

[m x 3.6]

[m/sec²]

0

X

0

0

1

5

1

X

5

2.5

1

5

2

X

X

10

10

2

-5

3

X

5

17.5

2

-5

4

X

0

20

<blank>

<blank>

  • The final A value has been kept blank, so that mean values per-phase add up, and phases no longer overlap.

mean values for ramp-up/down cycle, above

mean(V)

mean(S)

mean(A)

[kmh]

[m x 3.6]

[m/sec²]

phase1:

5

10

5

phase2:

5

10

-5

  • Applying the V-phasings and the extra 0 on mean(A) would have arrived to counterintuitive values, that don’t even sum up to 0:

    • up-ramp: \(\left(\frac{5 + 5 + (-5)}{3} =\right) 1.66m/sec^2\)

    • down-ramp: \(\left(\frac{(-5) + (-5) + 0}{3} =\right) -3.33m/sec^2\)

6.1.1.5. Practical deliberations

All phases in WLTC begin and finish with consecutive zeros(0), therefore the deliberations above do not manifest as problems; but at the same time, discovering off-by-one errors & shifts in time (wherever this really matters e.g. for syncing data), on arbitrary files containing calculated and/or measured traces is really hard: SUMs & CUMSUMs do not produce any difference at all.

The tables in the next section, along with accompanying CRC functions developed in Python, come as an aid to the problems above.

6.1.1.6. Phase boundaries

As reported by wltp.cycles.cycle_phases(), and neglecting the advice to optionally add a final 0 when calculating the cycle Acceleration (Annex 1 2-3.1), the following 3 phasing are identified from velocity traces of 1Hz:

  • V: phases for quantities dependent on Velocity samples, overlapping split-times.

  • VA0: phases for Acceleration-dependent quantities, -1 length, NON overlapping split-times, starting on t=0.

  • VA1: phases for Acceleration-dependent quantities, -1 length, NON overlapping split-times, starting on t=1. (e.g. Energy in Annex 7).

class

phasing

phase-1

phase-2

phase-3

phase-4

class1

V

[0, 589]

[589, 1022]

[1022, 1611]

VA0

[0, 588]

[589, 1021]

[1022, 1610]

VA1

[1, 589]

[590, 1022]

[1023, 1611]

class2

V

[0, 589]

[589, 1022]

[1022, 1477]

[1477, 1800]

VA0

[0, 588]

[589, 1021]

[1022, 1476]

[1477, 1799]

VA1

[1, 589]

[590, 1022]

[1023, 1477]

[1478, 1800]

class3a

V

[0, 589]

[589, 1022]

[1022, 1477]

[1477, 1800]

VA0

[0, 588]

[589, 1021]

[1022, 1476]

[1477, 1799]

VA1

[1, 589]

[590, 1022]

[1023, 1477]

[1478, 1800]

class3b

V

[0, 589]

[589, 1022]

[1022, 1477]

[1477, 1800]

VA0

[0, 588]

[589, 1021]

[1022, 1476]

[1477, 1799]

VA1

[1, 589]

[590, 1022]

[1023, 1477]

[1478, 1800]

6.1.1.7. Checksums

  • The crc_velocity() function has been specially crafted to consume series of floats with 2-digits precision (v_decimals) denoting Velocity-traces, and spitting out a hexadecimal string, the CRC, without neglecting any zeros(0) in the trace.

  • The checksums for all Phases (the problem) are reported by cycle_checksums(), and the the table below is constructed. The original checksums of the GTR are also included in the final 2 columns.

  • Based on this table of CRCs, the identify_cycle_v_crc() function tries to match and identify any given Velocity-trace:

CRCs & CUMSUMs for all phases over different “phasings”

CRC32

SUM

by_phase

cumulative

by_phase

cumulative

phasing⇨ phase⇩

V

VA0

VA1

V

VA0

VA1

V

V

class1

phase1

9840

4438

97DB

9840

4438

97DB

11988.4

11988.4

phase2

8C34

8C8D

D9E8

DCF2

090B

4295

17162.8

29151.2

phase3

9840

4438

97DB

6D1D

4691

F523

11988.4

41139.6

class2

phase1

8591

CDD1

8A0A

8591

CDD1

8A0A

11162.2

11162.2

phase2

312D

391A

64F1

A010

606E

3E77

17054.3

28216.5

phase3

81CD

E29E

9560

28FB

9261

D162

24450.6

52667.1

phase4

8994

0D25

2181

474B

262A

F70F

28869.8

81536.9

class3a

phase1

48E5

910C

477E

48E5

910C

477E

11140.3

11140.3

phase2

1494

D93B

4148

403D

2487

DE5A

16995.7

28136.0

phase3

8B3B

9887

9F96

D770

3F67

2EE9

25646.0

53782.0

phase4

F962

1A0A

5177

9BCE

9853

2B8A

29714.9

83496.9

class3b

phase1

48E5

910C

477E

48E5

910C

477E

11140.3

11140.3

phase2

AF1D

E501

FAC1

FBB4

18BD

65D3

17121.2

28261.5

phase3

15F6

A779

015B

43BC

B997

BA25

25782.2

54043.7

phase4

F962

1A0A

5177

639B

0B7A

D3DF

29714.9

83758.6

… where if a some cycle-phase is identified as:

  • V phasing, it contains all samples;

  • VA0 phasing, it lacks -1 sample from the end;

  • VA1 phasing, it lacks -1 sample from the start.

6.1.1.8. Practical example

For instance, let’s identify the V-trace of class1’s full cycle:

>>> from wltp.datamodel import get_class_v_cycle  as wltc
>>> from wltp.cycles import identify_cycle_v as crc
>>> V = wltc("class1")

>>> crc(V)            # full cycle
('class1', None, 'V')
>>> crc(V[:-1])       # -1 (last) sample
('class1', None, 'VA0')

The crc() function returns a 3-tuple: (i-class, i-phase, i-kind):

  • When i-phase is None, the trace was a full-cycle.

Now let’s identify the phases of “Access-DB”:

>>> crc(V[:590])      # AccDB phase1 respects GTR
('class1', 'phase-1', 'V')
>>> crc(V[590:1023])  # AccDB phase2 has -1 (first) sample
('class1', 'phase-2', 'VA1')
>>> crc(V[:1023])     # cumulative AccDB phase2 respects GTR
('class1', 'PHASE-2', 'V')

  • When i-phase is CAPITALIZED, the trace was cumulative.

  • Phase2 is missing -1 sample from the start (i-kind == VA1).

>>> crc(V[1023:])     # AccDB phase3
('class1', 'phase-1', 'VA1')

  • Phase3 was identified again as phase1, since they are identical.

Finally, clipping both samples from start & end, matches no CRC:

>>> crc(V[1:-1])
(None, None, None)

To be note, all cases above would have had identical CUMSUM (GTR’s) CRCs.